CHƯƠNG I. LÝ THUYẾT XÁC SUẤT VÀ SUY LUẬN

Trong thực tế thường xảy ra các hiện tượng khác nhau mang tính chất ngẫu nhiên, chẳng hạn: Số người đến khám bệnh trong ngày ở một phòng khám; số các vụ tai nạn xe cộ trong một năm ở một nước .... Việc nghiên cứu các hiện tượng ngẫu nhiên là vấn đề quan trọng, có tác dụng tìm hiểu và cải tạo thiên nhiên để phục vụ lợi ích con người.

Lý thuyết xác suất là ngành toán học nghiên cứu tính qui luật của các hiện tượng ngẫu nhiên.

I. PHÉP THỬ VÀ BIẾN CỐ:

Trong tự nhiên và xã hội, mỗi một hiện tượng đều gắn liền với một nhóm các điều kiện cơ bản và các hiện tượng đó có thể xảy ra khi nhóm các điều kiện cơ bản gắn liền với nó được thực hiện. Do đó, khi muốn nghiên cứu một hiện tưựng, ta cần thực hiện nhóm các điều kiện cơ bản ấy. Chẳng hạn, nếu muốn quan sát việc xuất hiện mặt sấp hay mặt ngửa của một đồng xu, ta phải tung đồng xu xuống mặt đất; khi muốn nghiên cứu chất lượng của một lô sản phẩm, ta phải lấy ngẫu nhiên một hoặc một số sản phẩm của lô đó để kiểm tra ...

Việc thực hiện một nhóm các điều kiện cơ bản để quan sát một hiện tượng nào đó có xảy ra hay không được gọi là thực hiện một phép thử, còn hiện tượng có thể xảy ra trong kết quả của phép thử đó dược gọi là biến cố.

Thí dụ 1 : Tung một con xúc xắc xuống đất là một phép thử; còn việc xuất hiện mặt nào đó là một biến cố. Cụ thế: xuất hiện mặt i chấm là một biến cố, chúng ta thường kí hiệu: Ai = {mặt i chấm xuất hiện khi gieo xúc xắc}.

Thí dụ 2: từ một lô sản phẩm gồm chính phẩm và phế phẩm, lấy ngẫu nhiên một sản phẩm. Việc lấy sản phẩm là một phép thử, còn lấy được chính phẩm hay phế phẩm là biến cố. Cụ thể ta có thể kí hiệu:

A = { lấy được chính phẩm} ; B = { lấy được phế phẩm}

Như vậy, ta thấy rằng một biến cố chỉ có thể xảy ra khi một phép thử gắn liền với nó được thực hiện.

Trong thực tế có thể xảy ra các loại biến cố sau đây:

  • Biến cố chác chắn: là biến cố nhất định sẽ xảy ra khi thực hiện một phép thử, biến cố chắc chắn thường được kí hiệu là U;

      Thí dụ: khi gieo con xúc xắc ta có: U = {xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 6}.

  • Biến cố không thể có (gọi tắt là biến cố không thể): là biến cố nhất định không xảy ra khi thực hiện một phép thử. Biến cố không thể kí hiệu bằng chữ

  • Biến cố ngẫu nhiên: là biến cố có thể xảy ra hoặc không xảy ra khi thực hiện một phép thử.

II. PHÉP TOÁN VÀ QUAN HỆ CỦA CÁC BIẾN CỐ:

Về mặt toán học, việc nghiên cứu quan hệ và phép toán trên tập các biến cố cho phép ta xác định chúng thực chất hơn.

Định nghĩa 1 :Biến cố C được gọi là tổng (hay hợp) của hai biến cốAvà B, kí hiệu là C =A+ B, nếu C xảy ra khi có ít nhất một trong hai biến cố ấy xảy ra.

Định nghĩa2: Biến cố A được gọi là tổng của n biến cốA1,A2,..Annếu A xảy ra khi ít nhất có một trong n biến cố ấy xảy ra và kí hiệu: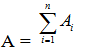

Gắn liền với khái niệm tổng các biến cố là khái về sự xung khắc củacác biến cố.

Định nghĩa7: Hai biến cố A và B gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không làm thay đổi xác suất xảy ra củabiến cố kia và ngược lại.

Trong trường hợp việc biến cố' này xảy ra hay không xảy ra làm cho xác suất xảy ra của biến cố kia thay đổi thì hai biến cố đó được gọi là phụ thuộc nhau.

Quy tắc De Morgan.

Biến cố đối lập của một hợp thì bằng giao của các biến cố đối lập.

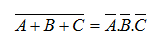
Biến cố đối lập của một giao thì bằng hợp của các biến cố đối lập.

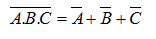
Qui tắc trên áp dụng cho một số hữu hạn bất kỳ các biến cố.

Chú ý: Các khái niệm về tổng, tích và hiệu của hai biến cố tương ứng với khái niệm phần bù, hợp, giao và hiệu của hai tập hợp.

III. CÁC ĐỊNH NGHĨA XÁC SUẤT CỦA MỘT BIẾN CỐ:

Như trên đã thấy, việc biến cố ngẫu nhiên xảy ra hay không xảy ra trong kết quả của phép thử là điều không thể đoán trước được. Tuy nhiên, bằng trực quan ta có thể nhận thấy các biến cố ngẫu nhiên khác nhau có những khả năng xảy ra khác nhau. Hơn nữa, khi lặp đi lặp lại nhiều lần cùng một phép thử trong những điều kiện như nhau người ta thấy tính chất ngẫu nhiên của các biến cố mất dần đi và khả năng xảy ra của biến cố sẽ được thể hiện theo những qui luật nhất định. Từ đó ta thấy có khả năng định lượng (đo lường) khả năng khách quan xuất hiện mộl biến cố nào đó.

Xác suất của một biến cố là một con số đặc trưng khả năng khách quan xuất hiện biến cố đó khi thực hiện phép thử.

3.1. Định nghĩa xác suất cổ điển:

Xác suất xuất hiện biến cố A trong một phép thử là tỷ số giữa số kết cục thuận lợi cho A và tổng số các kết cục duy nhất đồng khả năng có thể xảy ra khi thực hiện phép thử đó.

Nếu kí hiệu P(A) là xác suất xuất hiện biến cố A; m là số trường hợp thuận lợi cho A; n là số trường hợp đồng khả năng của phép thử (gọi tắt là số có thể) thì ta có công thức tính như sau:

3.2. Định nghĩa hình học của xác xuất

Giả sử có vô hạn kết cục đồng khả năng của một phép thử. Trong trường hợp này chúng ta có thể biểu thị bởi một miền hình học G (chẳng

hạn một đoạn thẳng, một miền mặt công, hoặc khối không gian...). Còn

tập các kết cục thuận lợi cho A biểu thị bới một miền con S nào đó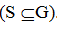

Sẽ rất hợp lý nếu ta định nghĩa xác suất là tỷ số số đo của S và G. Như vậy ta có P(A) bằng xác suất để một điểm gieo rơi vào miền S với giả thiết nó có thể rơi đồng khả năng vào các điểm của miền G và ta có công thức:

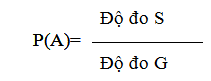
3.3. Định nghĩa thống kê về xác suất.

a) Định nghĩa tần suất:

Tần suấtxuấthiện biến cố trong n phép thử là tỷ số giữa số phép thử mà trong dó biến cố xuất hiện và tổng số phép thử được thực hiện.

Như vậy, nếu kí hiệu số phép thử được thực hiện là n, số ỉần xuất hiện biến cố A là k thì tần suất xuất hiện biến cố A là f(A) thì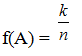

IV. CÁC ĐỊNH LÍ VỀ XÁC SUẤT CỦA MỘT BIẾN CỐ:

4.1. Định lí nhân xác suất:

a) Xác suất có điều kiện

Định nghĩa: Xác suất của biến cố A được tính với điều kiện biến cố B đã xảy ra gọi là xác suất có điều kiện của A và kí hiệu là P(A/B).

b) Định lí nhân xác suất:

Định lí 1: Xác suất của tích hai biến cố A và B bằng tích xác suất của một trong hai biến cố đó với xác suất có điều kiện của biến cố còn lại.

P(AB) = P(A).P(B/A) = P(B).P(A/B).

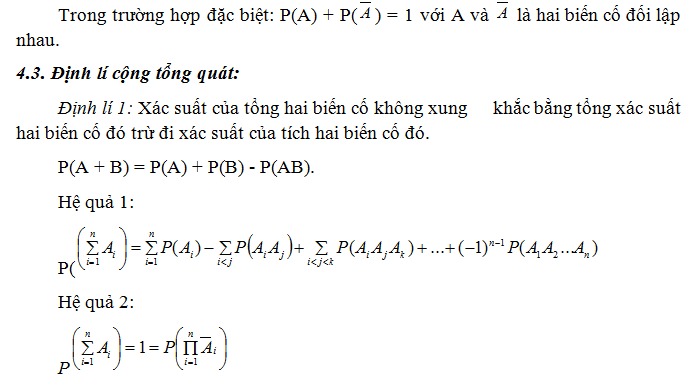V. DÃY PHÉP THỬ BERNOULLI

5.1. Định nghĩa:

Tiến hành n phép thử độc lập (tức là các kết quả của phép thử này không ảnh hưởng gì đến kết quả của phép thử kia) được gọi là n phép thử Bernoulli (hoặc một lược đồ Bernoulli) nếu thỏa mãn hai điều kiện:

(1) Mỗi phép thử có 1 trong hai kết cục là A hoặc 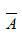xuất hiện.

(2) P(A) = p; P(A) như nhau đối với mỗi phép thử.

Thí dụ: Gieo một đồng tiền 10 lần, đó là 10 phép thử Bernoulli; Gieo một con xúc xắc 100 lần, A = {mặt sáu chấm xuất hiện}. Đó là 100 phép thử Bernoulli.

5.2. Xác xuất xuất hiện biến cố A:

Ta tìm xác xuất sao cho trong n phép thử Bernoulli, biến cố A xuất hiện m lần. Ký hiệu xác xuất này là Pn(m,p), Ta có:

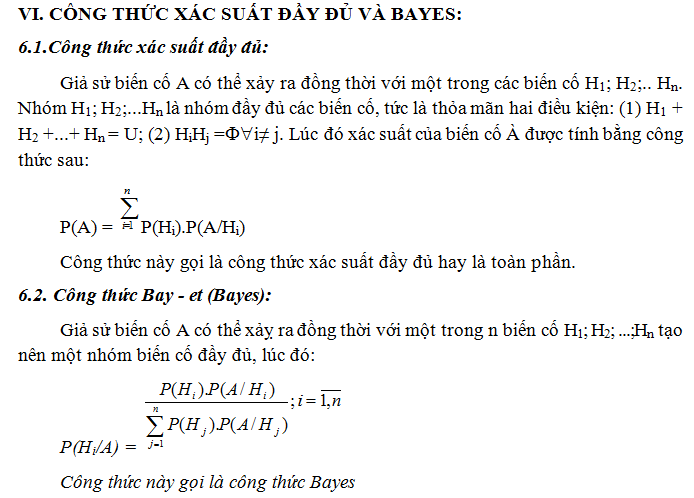
VII. BIẾN NGẪU NHIÊN

1.Định nghĩa:

Một biến số được gọi là biến ngẫu nhiên nếu trong kết quả của phép thử nó sẽ  nhận một và chỉ một trong các giá trị có thể có của nó với một xác suất tương ứng xác định, được kí hiệu là X, Y, Z,.. hoặc X1, X2, X3…

Các giá trị có thể có của biến X được kí hiệu là: x1, x2, x3,…

Khi 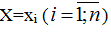nó trở thành biến ngẫu nhiên với xác suất xác định.

  1. Phân loại biến ngẫu nhiên:

    • Biến ngẫu nhiên gọi là rời rạc nếu các giá trị có thể có của nó lập nên một tập hợp hữu hạn hoặc đếm được

    • Biến ngẫu nhiên gọi là liên tục nếu các giá trị có thể có của nó lấp đầy một khoảng trên trục số

  2. Bảng phân phối xác suất

    Bảng phân phối xác suất dùng để mô tả quy luật phân phối xác suất của biến ngẫu nhiên rời rạc.

Giả sử biến ngẫu nhiên rời rạc X có thể nhận các giá trị: x1, x2, ….,xn với các xác suất tương ứng là: p1, p2,…., pn. Ta lập bảng sau:

4.3. Ý nghĩa của hàm phân phối xác suất :

Từ định nghĩa hàm phân phối xác suất F(x) = P(X < x) nên giá trị của hàm phân phối xác suất tại một điểm x cho thấy có bao nhiêu phần của một đơn vị xác suất ( do toàn bộ xác suất của biến ngẫu nhiên bằng 1) phân phối trên đoạn ( - ∞ ; x)

  1. Hàm mật độ xác suất :

5.1. Định nghĩa: Hàm mật độ xác suất của biến ngẫu nhiên liên tục X ( ký hiệu là f(x)) là đạo hàm bậc nhất của hàm phân phối xác suất của biến ngẫu nhiên đó.

       F'(x) = f(x)

5.2.Các tính chất:

Tính chất 1: Hàm mật độ xác suất luôn không âm: f(x) ≥ 0 với mọi x

Tính chất 2: Xác suất để biến ngẫu nhiên liên tục X nhận giá trị trong khoảng (a;b) bằng tích phân xác định của hàm mật độ xác suất trong khoảng đó:

CHƯƠNG 2: PYTHON VÀ ỨNG DỤNG TRONG LẬP TRÌNH XÁC SUẤT

I. TÌM HIỂU VỀ PYTHON

1.Lịch sử Python

Python được phát triển bởi Guido Van Rossum vào cuối những năm 80 và đầu những năm 90 tại Viện toán-tin ở Hà Lan. Python kế thừa từ nhiều ngôn ngữ như ABC, Module-3, C, C++, Unix Shell, …

Ngôn ngữ Python được cập nhật khá thường xuyên để thêm các tính năng và hỗ trợ mới. Phiên bản mới nhất hiện nay của Python là Python 3.3 được công bố vào 29/9/2012 với nguyên tắc chủ đạo là "bỏ cách làm việc cũ nhằm hạn chế trùng lặp về mặc chức năng của Python".

2.Khái niệm Python

Python là một ngôn ngữ lập trình bậc cao, thông dịch, hướng đối tượng, đa mục đích và cũng là một ngôn ngữ lập trình động.

Cú pháp của Python là khá dễ dàng để học và ngôn ngữ này cũng mạnh mẽ và linh hoạt không kém các ngôn ngữ khác trong việc phát triển các ứng dụng. Python hỗ trợ mẫu đa lập trình, bao gồm lập trình hướng đối tượng, lập trình hàm và mệnh lệnh hoặc là các phong cách lập trình theo thủ tục.

Python không chỉ làm việc trên lĩnh vực đặc biệt như lập trình web, và đó là tại sao ngôn ngữ này là đa mục đích bởi vì nó có thể được sử dụng với web, enterprise, 3D CAD, …

Bạn không cần sử dụng các kiểu dữ liệu để khai báo biến bởi vì kiểu của nó là động, vì thế bạn có thể viết a=15 để khai báo một giá trị nguyên trong một biến.

Với Python, việc phát triển ứng dụng và debug trở nên nhanh hơn bởi vì không cần đến bước biên dịch và chu trình edit-test-debug của Python là rất nhanh.

3.Đặc điểm của Python

-Dễ dàng để sử dụng: Python là một ngôn ngữ bậc cao rất dễ dàng để sử dụng. Python có một số lượng từ khóa ít hơn, cấu trúc của Python đơn giản hơn và cú pháp của Python được định nghĩa khá rõ ràng, … Tất cả các điều này là Python thực sự trở thành một ngôn ngữ thân thiện với lập trình viên.

-Bạn có thể đọc code của Python khá dễ dàng. Phần code của Python được định nghĩa khá rõ ràng và rành mạch.

-Python có một thư viện chuẩn khá rộng lớn: Thư viện này dễ dàng tương thích và tích hợp với UNIX, Windows, và Macintosh.

  • Python là một ngôn ngữ thông dịch: Trình thông dịch thực thi code theo từng dòng (và bạn không cần phải biên dịch ra file chạy), điều này giúp cho quá trình debug trở nên dễ dàng hơn và đây cũng là yếu tố khá quan trọng giúp Python thu hút được nhiều người học và trở nên khá phổ biến.

-Python cũng là một ngôn ngữ lập trình hướng đối tượng. Ngoài ra, Python còn hỗ trợ các phương thức lập trình theo hàm và theo cấu trúc.

Ngoài các đặc điểm trên, Python còn khá nhiều đặc điểm khác như hỗ trợ lập trình GUI, mã nguồn mở, có thể tích hợp với các ngôn ngữ lập trình khác, …

4.Chương trình Python cơ bản

<!--

Cách thực thi Python trong chế độ script

Sử dụng chế độ script, bạn cần viết Python code trong một file riêng rẽ bởi sử dụng bất cứ trình soạn thảo nào trong hệ điều hành của bạn. Sau đó, bạn lưu nó với đuôi .py và mở dòng nhắc lệnh để thực thi.

Giả sử bạn gõ source code sau trong một test.py file:

Nếu bạn đã có trình thông dịch của Python được thiết lập trong biến PATH, bây giờ bạn thử chạy chương trình trên như sau:

II. XÂY DỰNG MÔ HÌNH CƠ BẢN SỬ DỤNG NAVIE BAYES TRONG PYTHON

Có 3 kiểu mô hình Navie Bayes:

-Gaussian: Nó được sử dụng trong phân loại và nó giả định rằng các tính năng đi theo 1 phân bố bình thường.

-Multinomial: Nó được dùng cho các phép tính rời rạc. Ví dụ: Phân loại văn bản, đếm bao nhiêu từ xảy ra trong tài liệu, bạn có thể nghĩ về nó như là “số lần số kết quả x_i được quan sát qua n thử nghiệm”.

-Bernoulli: Mô hình nhị thức rất hữu ích nếu các vectơ tính năng của bạn là nhị phân. Một ứng dụng sẽ là phân loại văn bản với môhình“bag of words”, trong đó các chữ số 1 và số 0 là“từ xuất hiện trong tài liệu”và“từ không xuất hiện trong tài liệu”

Vì sao nên sử dụng Navie Bayes:

Navie Bayes là một lựa chọn tuyệt vời cho việc phân loại tài liệu vì nó khá nhanh, nó có thể xử lý một số lượng lớn các tính năng ( nghĩa là từ), và nó thực sự hiệu quả.

CHƯƠNG III. MINH HỌA QUA BÀI TOÁN CỤ THỂ

I.BÀI TOÁN PHÂN LOẠI TÀI LIỆU (DOCUMENT CLASSICFICATION)

Đối với ví dụ sau đây, chúng ta sẽ phân loại xem một trang wikipedia có đề cập đến một con khủng long(Dino)hay mộtsinh vật bí ẩn (Crypto). (https://en.wikipedia.org/wiki/Cryptozoology)

Chúngtasẽ sử dụng văn bản từ mỗi bài viết wikipedia làm các tính năng. Những gì chúng ta mong đợi là những từ nhất định như "sighting" hay "hoax" thường được tìm thấy trong các bài báo về khoa học cryptozoology, trong khi những từ như "fossil" thường được tìm thấy trong các bài viết về khủng long.

Chúng tasẽ thực hiện một số từ cơ bản để đếm số lần xuất hiện của mỗi từ và sau đó tính toán xác suất điều kiện cho mỗi từ liên quan đến 2 loại đó.

Cụ thể:

Tập huấn luyện : Dino, Crypto

Dino: có 7 file (tương ứng với 7 con) là chi là khủng long

Cryto: có 8 file (tương ứng với 8 con) là các sinh vật bí ẩn

Tập test: Yeti (mô tả về con yeti dự đoán nó thuộc chi khủng long hay là thuộc sinh vật bí ẩn)

Ý TƯỞNG

Gọi D: biến cố chỉ con Dino

C: biến cố chỉ conCryto

Y: biến cố chỉ con Yeti

Ta tính

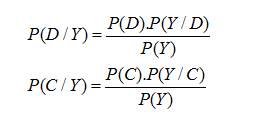
Sau đó so sánh P(D/Y) và P(C/Y) từ đó đi đến kết luận.

Tiếp theo:Tính P(Y/D); P(Y/C)

-Ta tiến hành đếm số từ vựng xuất hiện trong các file dữ liệu của con Yeti. Từ đó tính xác suất xuất hiện của từ vựng đó trong file Yeti. P-word=số lần xuất hiện của từ đó/tổng số từ trong file.

-Tính xác suất xuất hiện từ vựng đó trong file Dino P(w/D)

Vấn đề là làm thế nào để tính được các xác suất trên?

Bước1: Tính P(D) và P(C)

Trong vi dụ này ta có 15 file huấn luyện, trong đó có 7 file dino và 8 file Crypto, như vậy

P(D)=số file của Dino/tổng số file huấn luyện (7/15)

P(C)= số file của Crypto/tổng số file huấn luyện (8/15)

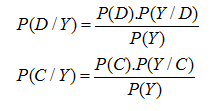
So sánh P(D/Y) và P(C/Y)

-Nếu P(D/Y)>P(C/Y) thì kết luận khả năng đó là con Dino

-Nếu P(D/Y)<P(C/Y) thìkết luận khả năng đó là con Crypto

Thực hiện với Python

Tokenizing vàcounting

Điều đầu tiên chúng ta nghĩ đến làbiến các tập tin của chúng ta thành văn bản thành một số ít toán học. Điều đó có nghĩa là chúng ta sẽ đếm bao nhiêu lần mỗi từ xuất hiện trong mỗi tài liệu. Chúng tacũng sẽ thực hiện việc bình thường hóa văn bản nhỏ bằng cách loại bỏ dấu câu và giảm văn bản (điều này có nghĩa là "Hello" và "hello" bây giờ sẽ được coi là cùng một từ).

Một khi chúng tađã đưa văn bản về theo một chuẩn, chúng ta cần một cách để mô tả từ. Một cách tiếp cận đơn giản là sử dụng một good 'ole regex tốt mà chia tách trên khoảng trắng và dấu chấm câu: W +.

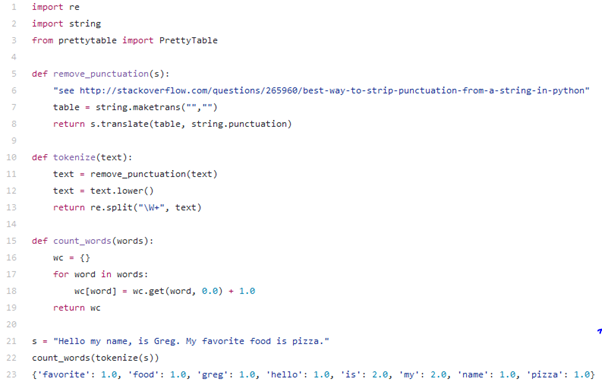
Tính xác suất(Caculating Probabilities)

Bâygiờ chúng ta có thể đếm từ.Codedưới đây sẽ làm như sau:

Mở từng tài liệu.

Dán nhãn nó là "crypto" hoặc "dino" và theo dõi xem có bao nhiêu trong mỗi nhãn có(priors).

Tính từ cho tài liệu.

Thêm các giá trị đó vào vocab, hoặc đếm từ mức nội bộ.

Thêm các giá trị đó vào cácword_counts, choviêc đếm các từ loại.

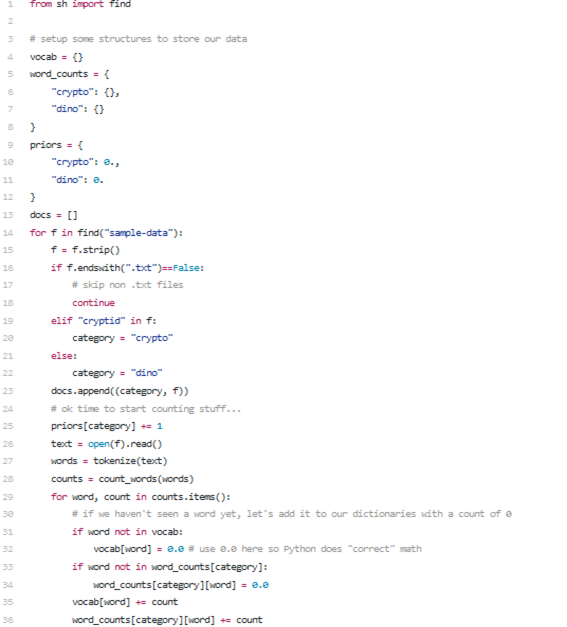
Phân loại một trang mới

Và cuối cùng là thời gian cho toán học. Chúng ta sẽ sử dụng số đếm từ chúng ta tính trong bước trước để tính toán như sau:

Prior Probabilitycho mỗi loại, phần trăm các tài liệu thuộc về mỗi loại. Chúng tacó 9 tài liệu mật và 8 tài liệu dino, do đó cho chúng ta những điều sau đây:

Điều tiếp theo chúng ta cần là xác suất có điều kiện cho các từ trong tài liệu mà chúng ta đang cố gắng phân loại, làm sao chúng ta làm việc đó bây giờ? Chúng ta bắt đầu bằng cách đếm từ trên một tài liệu mới. Chúng tasẽ sử dụng trang Yeti làm tài liệu mới của chúng ta.

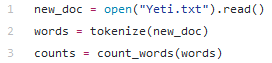
Bây giờ chúng ta sẽ tính toán P (word | category) cho mỗi từ và nhân cho mỗi xác suất có điều kiện với nhau để tính P (category | set of words). Để tránh lỗi tính toán, chúng ta sẽ thực hiện các thao tác trong logspace.

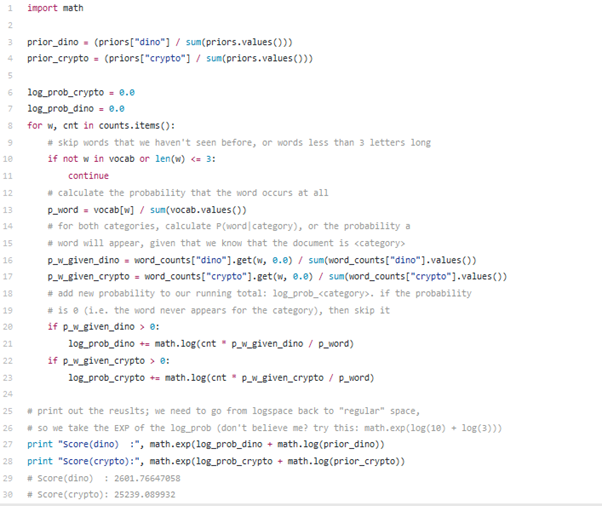
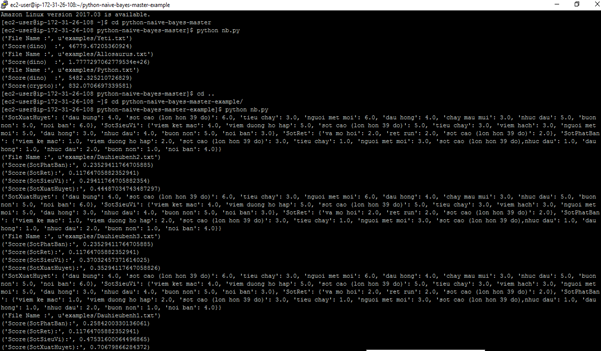
Kết quả sau khi phân loại:

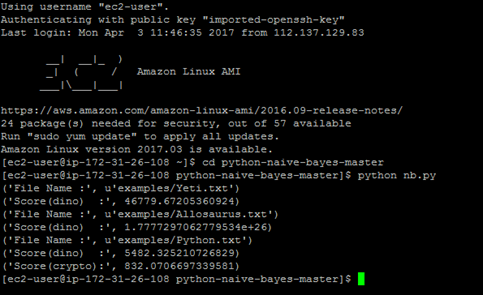
II.BÀI TOÁN PHÂN LOẠI DỰA TRÊN DẤU HIỆU ĐỘC LẬP

Xây dựng một hệ chuyên gia, mô phỏng cách thức tư duy của người thầy thuốc để hỗ trợ chuẩn đoán phân biệt các bệnh sốt.

Bài toán:

input: một số triệu chứng mà bệnh nhân gặp phải.

output: Dự đoán bênh sốt mà bệnh nhân có khả năng bị

Ý tưởng:

Các bước tiến hành

Lập cơ sở dữ liệu để đào tạo cho máy:

-Tiến hành thu thập số liệu từ phòng khám của Ban bảo vệ sức khỏe cán bộ Hà nội (25 bộ)

Dạy cho máy:

-Sử dụng công thức xác suất để tính các xác suất tiền nghiệm: P(Aj); P(K/Aj); P(K)

Chuẩn đoán kết quả:

-Dựa vào triệu chứng K của người bệnh: tính các xác suất hậu nghiệm: P(Aj/K). So sánh các xác suất hậu nghiệm đó xem xác xuất nào là lớn nhất và từ đó kết luận khả năng lớn nhất bệnh nhân đang mắc phải bệnh nào.

Dữ liệu thu thập được

-Bộ 1: gồm 17 trường hợp dùng cho huấn luyện.

-Bộ 2: gồm 8 trường hợp dùng cho kiểm thử

Bảng tóm tắt 17 trường hợp bị sốt cao dùng cho huấn luyện.

Từ các dữ liệu này, ta nhập vào máy dưới dạng mảng dữ liệu: A[i;j]

i: () biến chỉ các loại bệnh lần lượt: Sốt phát ban; sốt xuất huyết; sốt rét; sốt siêu vi

j: () các dấu hiệu gặp phải lần lượt: sốt cao (>=39 độ);người mệt mỏi; nhức đầu; đau họng; đau bụng; buồn nôn; tiêu chảy; chảy máu mũi; nổi ban; rét run; vã mồ hôi; Viêm kết mạc; Viêm hạch; viêm đường hô hấp.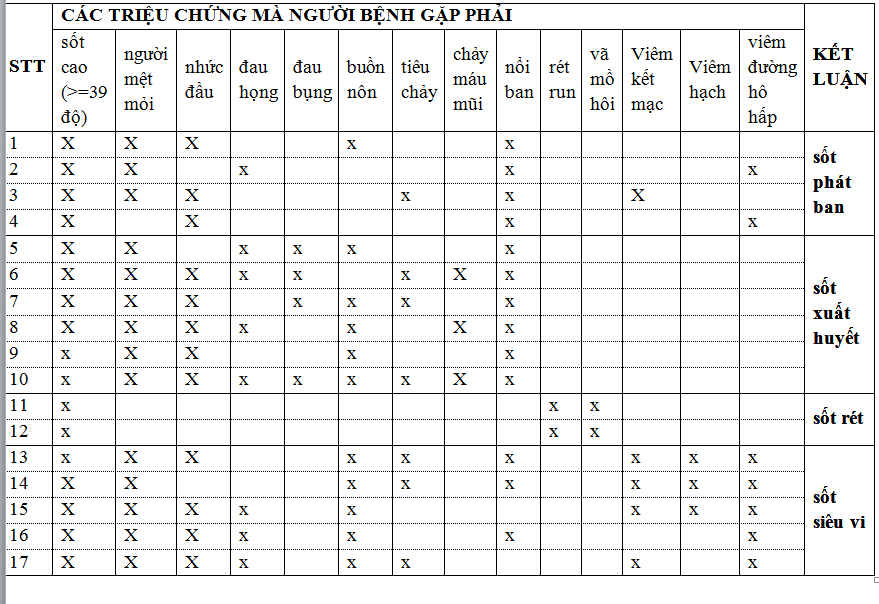

Tiến hành dạy cho máy.

-Ta thiết lập các công thức để tính toán các xác suất sau:

P(SPB)=4/17; P(SR)=2/17; P(SSV)=5/17; P(SXH)=6/17.

-Dựa vào các triệu chứng (H) gặp phải của bệnh nhân, ta tiến hành tính các xác suất

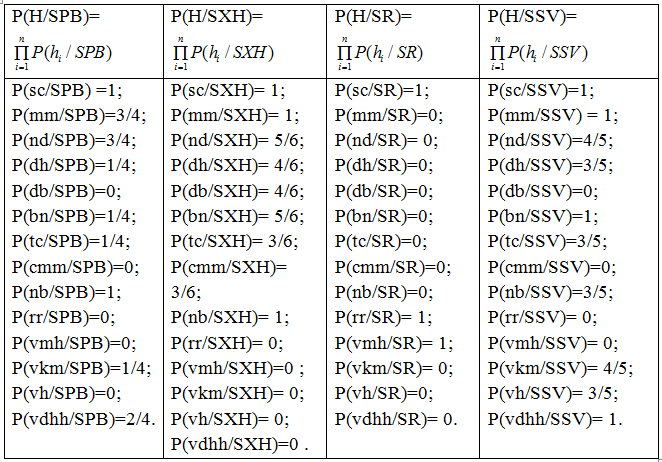
Như vậy ta tính được các kết quả :

P(H) = P(SPB).P(H/SPB)+ P(SXH).P(H/SXH)+ P(SR).P(H/SR)+ P(SSV).P(H/SSV)

= 4/17.P(H/SPB)+ 5/17.P(H/SXH)+2/17.P(H/SR)+6/17.P(H/SSV)

Kq1= P(SPB).P(H/SPB)/P(H)=4/17. P(H/SPB)/P(H);

Kq2= P(SXH).P(H/SXH)/P(H)=5/17. P(H/SXH)/P(H);

Kq3= P(SR).P(H/SR)/P(H)=2/17. P(H/SXH)/P(H);

Kq4= P(SSV).P(H/SSV)/P(H)=6/17. P(H/SSV)/P(H);

Ta tìm m=Max(Kq1; Kq2; Kq3; Kq4)

Nếu m=Kq1in ra KQ: {“ Bạn có khả năng bị Sốt Phát ban với xác suất mắc phải là”, Kq1}

Nếu m=Kq2in ra KQ: {“ Bạn có khả năng bị Sốt Xuất huyết với xác suất mắc phải là”, Kq2}

Nếu m=Kq3in ra KQ: {“ Bạn có khả năng bị Sốt Rét với xác suất mắc phải là”, Kq3}

Nếu m=Kq4in ra KQ: {“ Bạn có khả năng bị Sốt Siêu vi với xác suất mắc phải là”, Kq4}

Thực hiện với Python

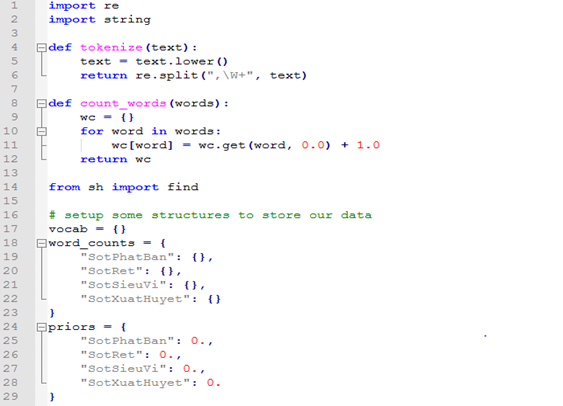
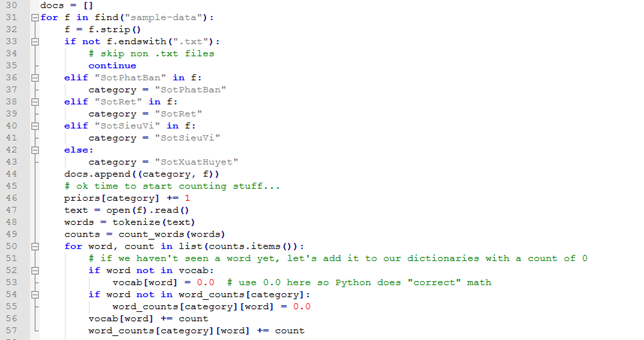
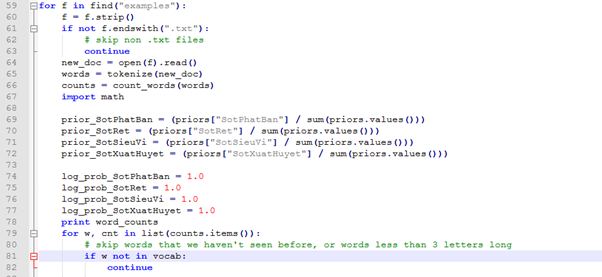
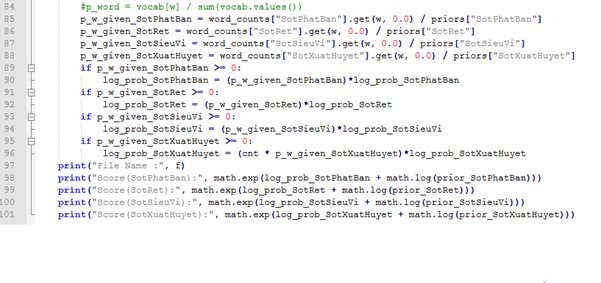
Kết quả thực hiện

results matching ""

    No results matching ""